Jack Wang
April 28th, 2003
The Doo-Sabin subdivision surface is a generalization of biquadratic B-splines, and can be rendered as tensor product patches except for at singularities. These singular points result from non 4-valent points and non-quadrilaterals on the control mesh. M. Sabin defined two patches in [1] to be used to replace the infinite regress found at the surface singular points in the case that the singularity is of valency 3 or 5. This project is an implementation of fitting Sabin patches along with tensor product patches onto the Doo-Sabin surface.
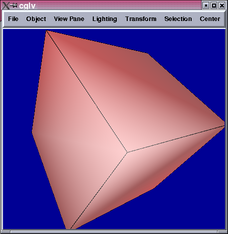
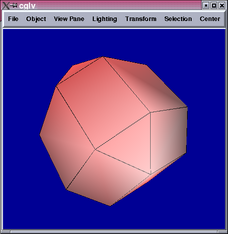
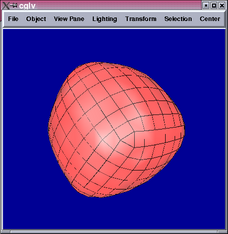
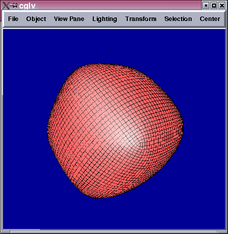
The implementation of Doo-Sabin subdivision required building a data
structure to access relevant adjacency information. I implemented
parts of the half-edge data structure to accomplish this. The following
are results from a cube with 0, 1, 3, and 5 levels of subdivision:
While it is possible to render the Doo-Sabin surface by subdividing
as many times as necessary, this approach is not without drawbacks.
Namely, like most other subdivision schemes, parametrization and evaluation
of points on the surface are not trivial [2].
One property of the Doo-Sabin subdivision is that each mesh point of valency 4 can be used to define a quadratic tensor product patch on the surface [1]. The 4 corners of the patch are given by the centroids of the 4 neighbouring faces to the mesh point. The 4 control points along the patch edges are given by the midpoints of the mesh edges that seperate the 4 faces, while the middle control point is the mesh point of valency 4 itself.
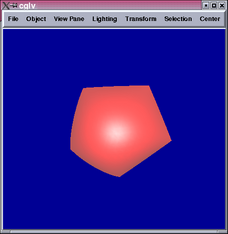
If we combine the above with another convenient property: every new
mesh point always have valency 4 [2], an alternative way of rendering
the surface follows. We could subdivide the initial mesh once, then
render a tensor product patch for each mesh point. Note that if we
subdivide the initial mesh more than once, we will just be fitting
more tensor product patches to the same surface. Below are
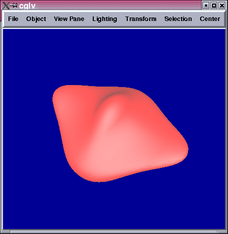
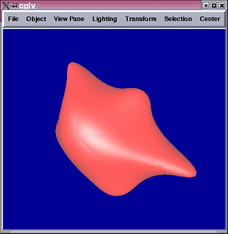
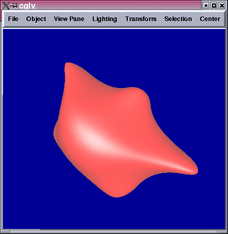
results using this method from different viewpoints.
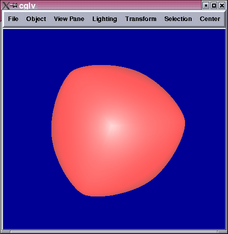
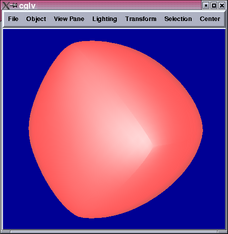
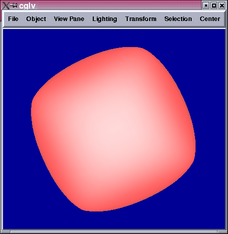
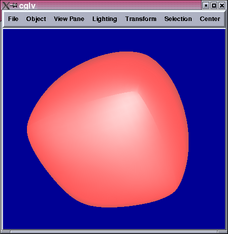
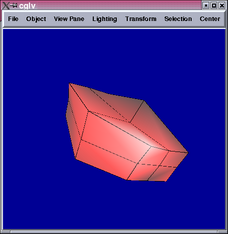
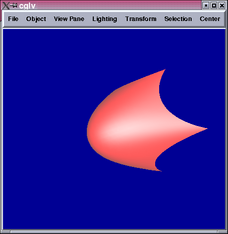
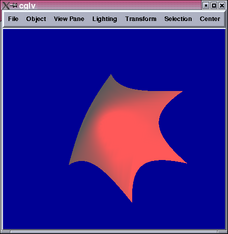
The 2nd and 4th images show parts of the tensor product patch network
are not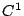 
.
A closer look reveals that the locations of the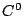 
portions correspond
to vertices of the initial cube, which all have valency 3. The subdivision
algorithm creates a 3-sided face from each vertex of the cube, and
each mesh point on the new face defines a tensor product patch. Hence,
3 tensor product patches meet at the centroid of each new face. This
means the 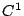conditions cannot be satisfied.
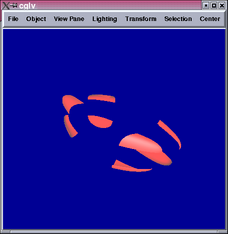
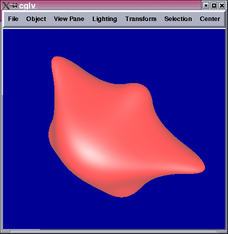
At this point, the use for Sabin patches is clear. Since vertices
of valency 3 on the initial mesh results in points on the surface
which cannot be fitted using tensor product patches with 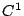continuity,
we identify these regions and directly fit 3-sided patches over them.
The cube from before is now constructed using 4 Sabin patches. The
details of Sabin patch control points can be found in [1].
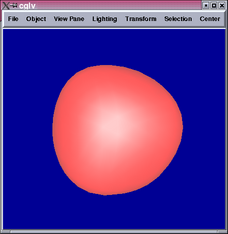
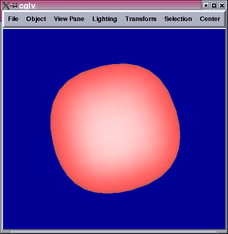
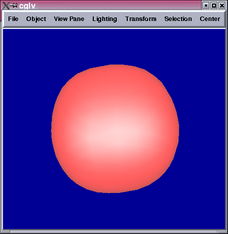
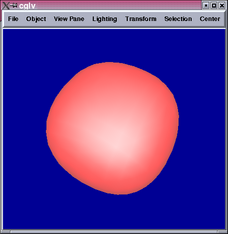
We see from the results above that the surface is completely and
seems to have less variance on curvature.
The Sabin patches are defined by points on the initial control mesh
before any subdivision [1], while tensor product patches require
1 level of subdivision to ensure each point have valency 4. To implement
this, I first generate all 3-sided Sabin patches from the initial
mesh. The surface is then subdivided once and all tensor product patches
are generated. Care must be taken here to ensure no tensor product
patches here overlap with any Sabin patch. One simple criteria is
to consider all neighbouring faces to a given vertex. If any of the
adjacent faces have 3 sides, then this vertex defines a tensor product
patch which overlaps a Sabin patch. Note a necessary assumption here
is that the initial mesh consists of only quadrilaterals (more about
this later).
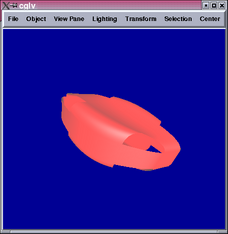
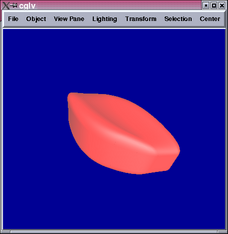
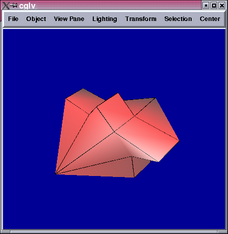
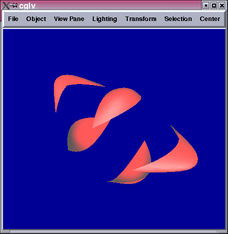
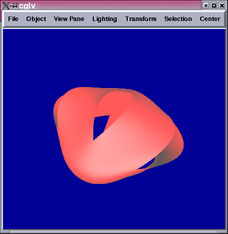
The first control mesh (top row) contains only vertices of valency
3 or 4, which the second contains a vertex of valency 5. Both results
demonstrate smooth connections between Sabin and tensor product patches.
The 5-valent vertex in the second control mesh is rendered with 5
tensor product patches, which leads to the same problem we had before
with the cube corner. To render this part of the surface properly,
we either have to use 5-sided Sabin patches or resort to pure subdivision.
The image on the right is from after 6 levels of subdivision, which
appears 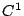everywhere. The left image demonstrates the 5-valent
singularity problem.
Much like the 3-sided patches before, control points for 5-sided patches
are defined on the initial mesh. The details of finding them can also
be found in [1]. Below are results for 5-sided patches fitting
nicely into the previous surface.
One annoying caveat of using Sabin patches to replace singularities is that once we see a non-quadrilateral face in the control mesh, it's already too late to replace it. Control points of Sabin patches come from neighbours of a 3 or 5-valent mesh point from one level before in the subdivision. Consequently, we are forced to assume the inital mesh consists of quadrilaterals only.
I thought that an interesting experiment to get around this problem would be to modify the initial mesh so that all faces become quadrilaterals. One way to do this is by subdivision, and the Catmull-Clark scheme has the property that all generated faces are 4-sided.
The adjacency information requirements for this scheme is very similar
to Doo-Sabin's. I was able to reuse my half-edge data structure from
before with only minor modifications.
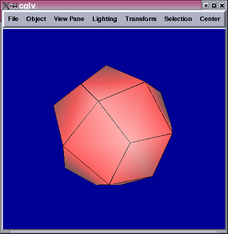
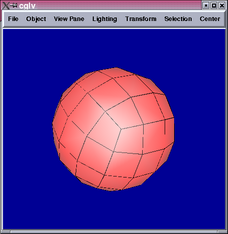
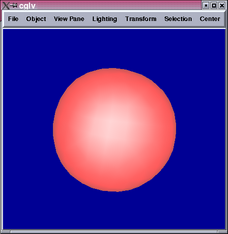
Catmull-Clark surface is a generalization of bicubic B-splines, the
results show that it fits a sphere much better than Doo-Sabin.
The control mesh is made of pure quadrilaterals after one level of Catmull-Clark subdivision. The patch-fitting algorithm now becomes:
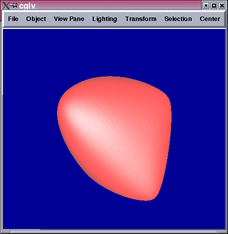
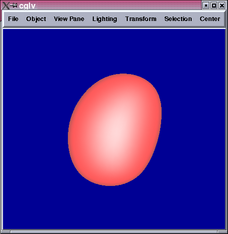
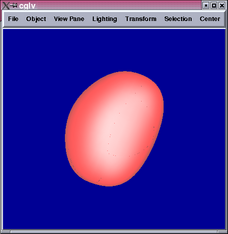
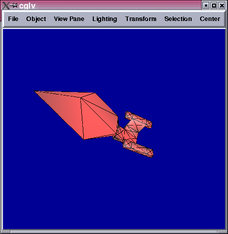
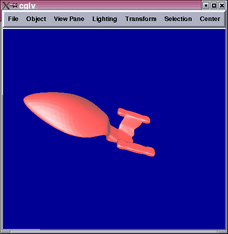
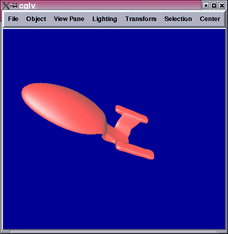
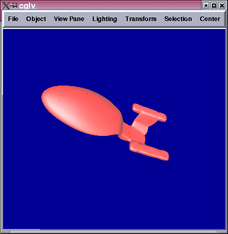
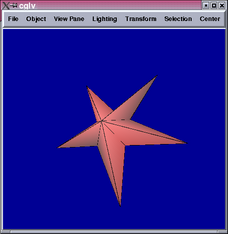
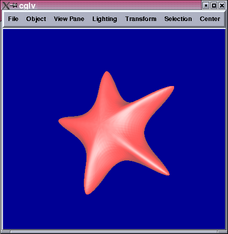
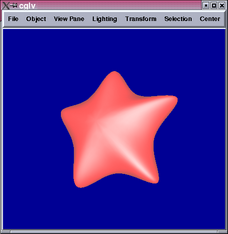
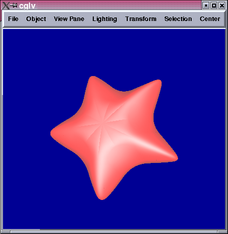
Generally speaking, the patch-fitting results appear to be between Doo-Sabin and Catmull-Clark surfaces in terms of smoothness. This is expected from the algorithm. We can see from the star example that singularity (10-valent) problems still exist in this patch fitting scheme and can be quite apparent. Sabin claims it is possible to replace higher valency singularities by combinations of 5-valent ones [1], which maybe worth investigating in the future.
I would like to acknowledge Prof. Stephen Mann for his help in providing the background information for the subject, and Bryan Chan for letting me use his home-made 3D models.
[1] M. Sabin, ``Non-rectangular surfaces suitable for inclusion
in a B-spline surface,'' in Proc. Eurographics, 1983, pp. 57-69.
[2] G. Farin, Curves and Surfaces for CAGD. Morgan Kaufmann Publishers,
2002.
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.48)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_subdir -split 0 -show_section_numbers /tmp/lyx_tmpdir18234dTzRxh/lyx_tmpbuf3/projectdoc.tex
The translation was initiated by Jack Wang on 2003-04-28