Adaptive Loop Subdivision

CS 779 (Winter 2020)
Ze Ran Lu

Adaptive Loop Subdivision

1. Base Project: Loop Subdivision

The base project is to implement Loop subdivision which can be applied the entire half-edge mesh without boundary only. First, the model is parsed and loaded as a half-edge mesh. The half-edge data structure provides easy access to neighbors.

First, the edge-flip and edge-split functions are implemented. The following images illustrates these functions.

Edge-flip

Edge-split

[Source of Image]

Then, for each (old) vertex, a new vertex position is computed based on the weighted average of itself all of its neighborhood, and is stored in the vertex structure, and for each (old) edge, a new vertex position is computed based the weighted average of itself and two common vertices of the endpoints, and is stored in the edge structure. Then, each edge is spitted, and new faces, edges, half-edges and vertices are created. Last, each new edge that connects a new vertex and old vertex is flipped. This completes one iteration.

1.1. Experiment: icosahedron.dae

Iteration	0	1	2	3	4
Output
Vertices	12	42	162	642	2562
Edges	30	120	480	1920	7680
Faces	20	80	320	1280	5120

2. (Extra) Boundary Support

2.1. Boundary Edge-split

In addition to the boundary case to compute the weighted average, the edge-split function must support the boundary case:
Edge-split for boundary

[Source of Image]

2.2. Fixing Boundary Vertices' Halfedges

It has been observed that each boundary vertex need to update its halfedge pointer to the halfedge linked with the outside of boundary ( a virtual face). The following pseudocode can fix the boundary:

for e in edges:
    if (e.isBoundary()):
        h = e.halfedge().twin()
        v = e.vertex()
        if v.halfedge() != h:
            v.set_halfedge(h)

2.3. Experiments

2.3.1. patch.dae

Iteration	0	1	2
Output
Vertices	16	49	169
Edges	33	240	456
Faces	18	72	288

2.3.2. hole.dae

Iteration	0	1	2	3
Output
Vertices	96	336	1248	4800
Edges	240	912	3552	14016
Faces	144	576	2304	9126

3. Crackless Adaptive Loop Subdivision

If we subdivide every face, the number of data grows exponentially, but if we subdivide a subset of faces, a crack may appear.

3.1. (Extra) Crack Prevention

If a triangle is not subdivided and the adjacent triangle is subdivided into four triangles, then a triangular crack would appear. If the subdivision levels differ by 1, we can bisect the coarse triangle to fill the hole. However, the edge-split function above automatically create faces, so a hole cannot exist. However, it still looks bad since it simply fill the triangular crack. We can fix it by unflipping the flipped edges that are the boundary of the faces selected for subdivision.

Before "unflip"	Find boundary edges	After "unflip"

The green area is the filled crack.	We need to locate the boundary of the faces selected for subdivision. This is located in the newEdge	Unflip the edge.

The following pseudocode shows the idea:

boundary = set()
for f in facesSelectedForSubdivision:
    for h in f.halfedges():
        boundary.insert(h)
        boundary.insert(h.twin())
for f in facesSelectedForSubdivision:
    for h in f.halfedges():
    boundary.remove(h)

# subdivide a subset of faces

for e in newEdges:
    if e.flipped and e.isConnectedTo(boundary):
        e.flip()
        assert(e.flipped == False)
    # some of the new edges are still "flipped", we can optionally clear the flag, because the edge will not be in the newEdges in the next iteration, it doesn't matter if it is marked as "flipped" or not. 
    e.flipped = False

3.2. Adaptive Subdivision

The adaptive subdivision based on the dihedral angle method described in the paper Adaptive Subdivision Schemes for Triangular Meshes.

The following pseudocode shows the idea:

def shouldSubdivide(face, threshold):
    faces = this.neighbors()
    if threshold == 0:
        return True
    for f in N:
        dotProduct = dot(f.normal(), this.normal()) # dot product of face unit normals
        angle = abs(acos(dotProduct)) # can use a value between 0 and 1 for threshold so we can skip the acos computation
        if angle > threshold:
            return True # if one of the angles is too acute
    return False

3.3. Experiments with Various Models

The s3d files can be found here. I only included the output image for subdivision level up to 2x because the visual difference is negligible if we go further. Bigger images below can be found by opening them in a new tab.

3.3.1. Experiment: bunny.dae

Iteration	0	1	2	3	4
Non-adaptive		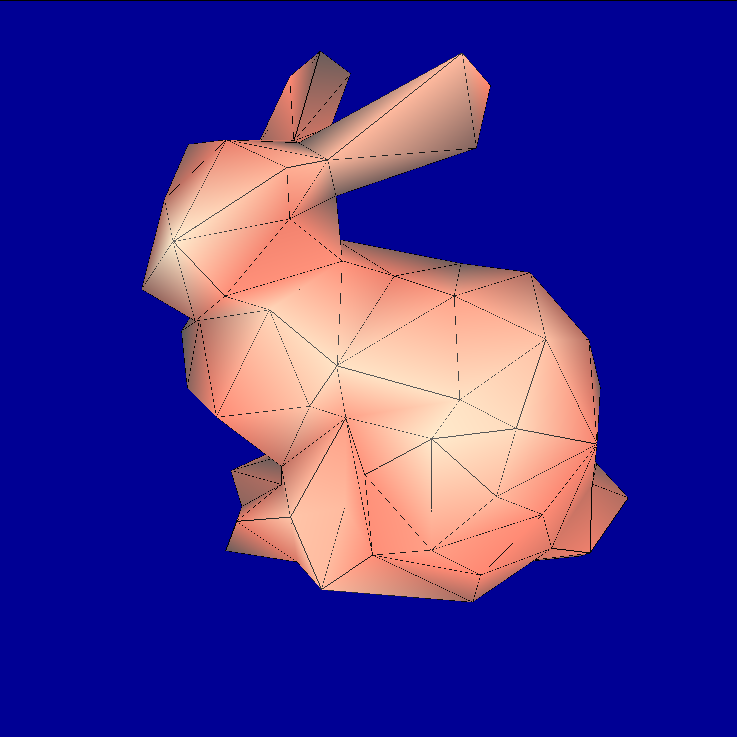		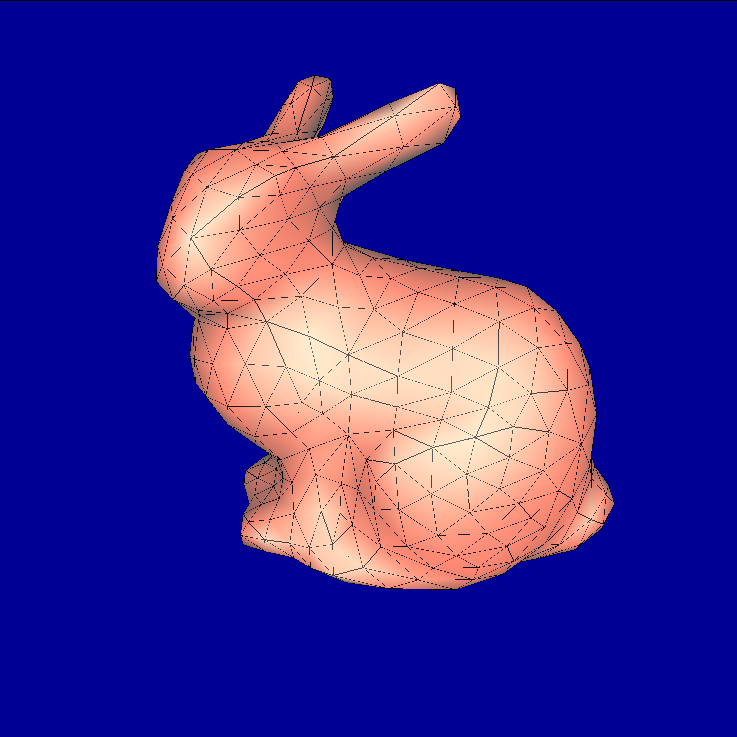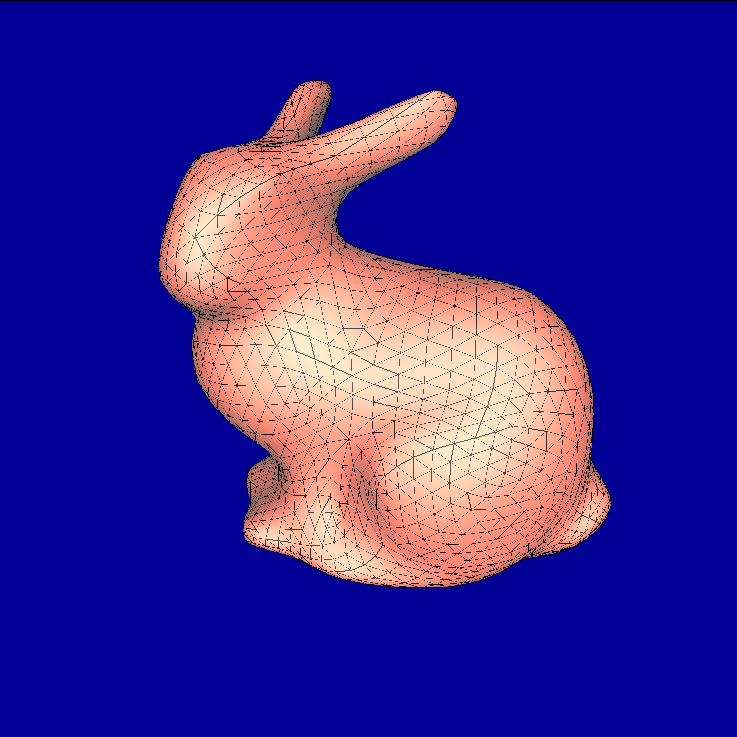N/A	N/A
Vertices	123	480	1890	7494	29838
Edges	357	1410	5604	22344	89232
Faces	232	928	3712	14848	59392

Adaptive with threshold = π/8	-		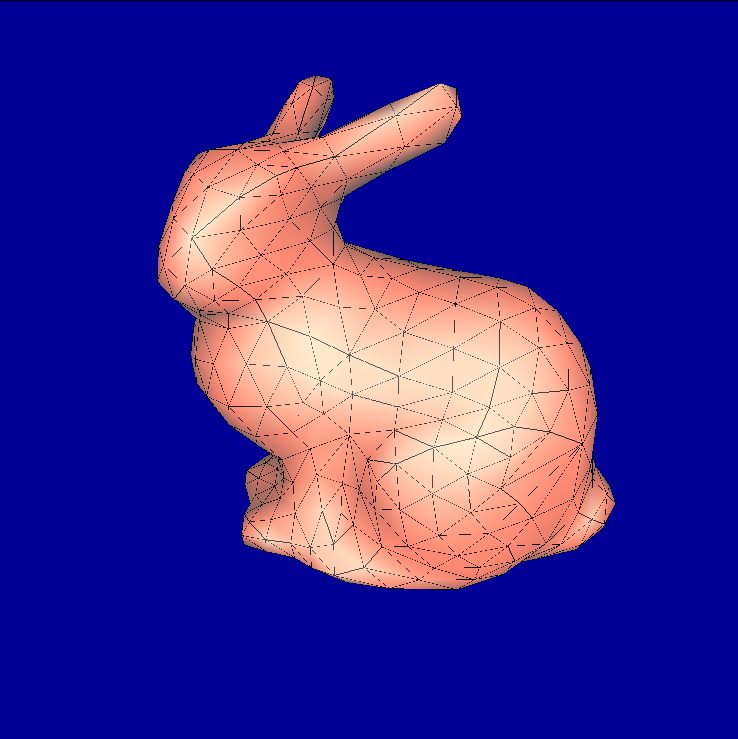	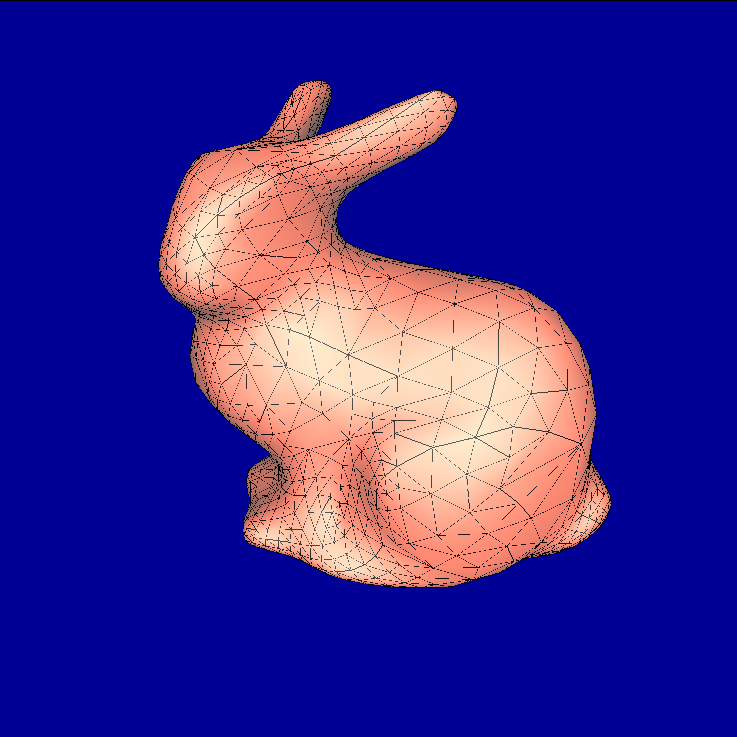N/A	N/A
Vertices	-	462	1247	2195	2878
Edges	-	1363	3709	6543	8579
Faces	-	899	2460	4346	5699
Ratio of triangles	1	0.97	0.66	0.29	0.10

2x non-adaptive	2x adaptive with threshold = π/8

3.3.2. Experiment: cat.dae

Iteration	0	1	2	3	4
Non-adaptive		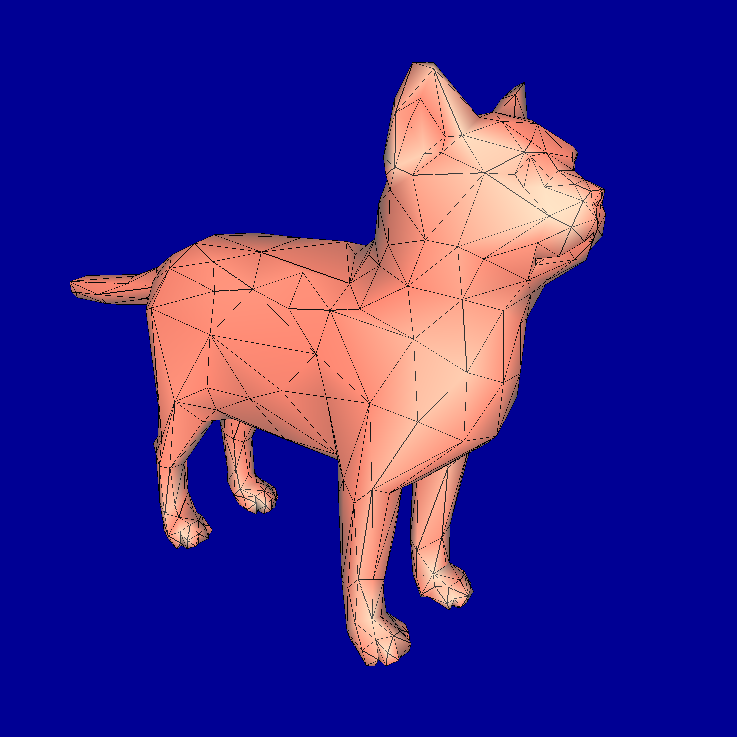		N/A	N/A
Vertices	509	2030	8114	32450	129794
Edges	1521	6084	24336	97344	389376
Faces	1014	4056	16224	64896	259584

Adaptive with threshold = π/8	-			N/A	N/A
Vertices	-	1906	4799	7324	8663
Edges	-	5712	14391	21966	25983
Faces	-	3808	9594	14644	17322
Ratio of triangles	1	0.94	0.59	0.23	0.07

2x non-adaptive	2x adaptive with threshold = π/8

3.3.3. Experiment: pooh.dae

Iteration	0	1	2	3	4
Non-adaptive				N/A	N/A
Vertices	522	2082	8322	33282	133122
Edges	1560	6240	24960	99840	399360
Faces	1040	4160	16640	66560	266240

Adaptive with threshold = π/8	-			N/A	N/A
Vertices	-	1980	5663	10999	17292
Edges	-	5934	16983	32991	51870
Faces	-	3956	11322	21994	34580
Ratio of triangles	1	0.95	0.68	0.33	0.13

2x non-adaptive	2x adaptive with threshold = π/8

4. Limitations and Extensions

4.1. High-valence Vertices

In Incremental Adaptive Loop Subdivision, the author suggests that repeatedly subdividing the same patches and using bisection method to remove cracks can yield high valence edges. Red-green triangularization was proposed to solve this problem.

4.2. Accurate Error Estimation

The dihedral angle method does not accurately estimate the error and the adaptive subdivision algorithm based on this still requires a user-defined maximum number of iteration. A tight error estimate of the maximum distance between a subdivision surface and its linear approximation was proposed in An Accurate Error Measure for Adaptive Subdivision Surfaces. Also, an adaptive subdivision based on limit surface normal was proposed in An Adaptive Subdivision Method Based on Limit Surface Normal. However, both algorithms require a precomputed dataset.

5. What I Learned

Manipulate half-edge data structure and apply this on Loop subdivision.
Fix the bad pointers of the boundary vertices resulted from the split and flip operations.
Understand the reason of cracks and how to fix them.
Calculate the boundary vertices from the selected faces.
Use the dihedral angle as a guide for adaptive subdivision.
Understand the reason of high-valence vertices.

5.1. What I Deserve Marks For

Support meshes with boundary.
Implement the adaptive subdivision based on dihedral angles.
Fix cracks.
Experiment with the adapive subdivision and the non-adaptive one and compare the number of primitives generated.
Subdivide various interesting models.

Acknowledgement

I would like to acknowledge Professor Stephen Mann for his help throughout the term. Also, my project is based on Scotty3D from CMU. It provided me convenience in many ways such as loading COLLADA files, rendering mesh using OpenGL and debugging.